Table Of Content
Next we can do the appropriate analysis for the fertilizer, recognizing that all the p-values for the plot effects are nonsense and should be ignored. Introduction to Statistics is our premier online video course that teaches you all of the topics covered in introductory statistics. Statology is a site that makes learning statistics easy by explaining topics in simple and straightforward ways. Our team of writers have over 40 years of experience in the fields of Machine Learning, AI and Statistics. For example, suppose researchers want to understand the effect that a new diet has on weight less.
Introduction to Time Series
The correct model specification contains the blocking factor before the treatment factor in the formula, and is y~block+drug for our example. This model adjusts treatments for blocks and the analysis is identical to an intra-block analysis for random block factors. The model y~drug+block, on the other hand, yields an entirely different ANOVA table and an incorrect \(F\)-test, as we discussed in Section 6.5. Each treatment occurs only once per block, and the variations due to interactions and residuals are completely confounded.
Example 8-10: Rice Data (Experimental Design)
If the experimenter focuses exclusively on the differences between treatments, the effects due to variations between the different blocks should be eliminated. Interpretation of the coefficients of the corresponding models, residualanalysis, etc. is done “as usual.” The only difference is that we do not test theblock factor for statistical significance, but for efficiency. Instead of a single treatment factor, we can also have a factorial treatmentstructure within every block. When I analyze the fertilizer, I have 32 experimental units (the thing I have applied my treatment to), but when analyzing the effect of irrigation, I only have 8 experimental units. A non-blocked way to run this experiment would be to run each of the twelve experimental wafers, in random order, one per furnace run. That would increase the experimental error of each resistivity measurement by the run-to-run furnace variability and make it more difficult to study the effects of the different dosages.
Table of contents
The calculator reports that the probability that F is greater than 4.4 equals about 0.04. To answer these questions, the researcher uses analysis of variance. Minitab’s General Linear Command handles random factors appropriately as long as you are careful to select which factors are fixed and which are random. The sequential sums of squares (Seq SS) for block is not the same as the Adj SS.
Lowering the thermal noise barrier in functional brain mapping with magnetic resonance imaging - Nature.com
Lowering the thermal noise barrier in functional brain mapping with magnetic resonance imaging.
Posted: Mon, 30 Aug 2021 07:00:00 GMT [source]
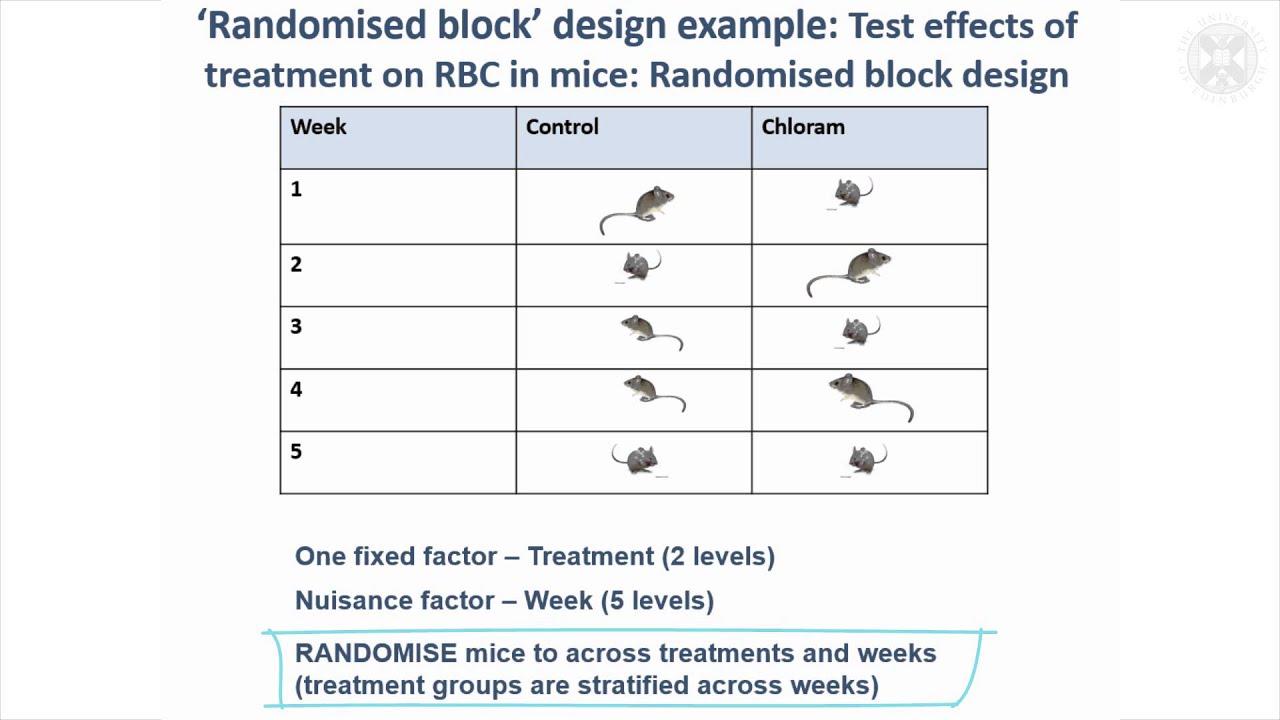
First we have 6 blocks and we’ll replicate the exact same experiment in each block. Within a block, we’ll split it into three sections, which we’ll call plots (within the block). We are interested in how a mouse responds to five different materials inserted into subcutaneous tissue to evaluate the materials’ use in medicine.
Interactions between climate change, urban infrastructure and mobility are driving dengue emergence in Vietnam - Nature.com
Interactions between climate change, urban infrastructure and mobility are driving dengue emergence in Vietnam.
Posted: Mon, 11 Dec 2023 08:00:00 GMT [source]
The vertical dispersion of the lines indicates that enzyme levels within each litter are systematically different from those in other litters. To be effective, blocking requires that we find some property by which we can group our experimental units such that variances within each group are smaller than between groups. Here is an actual data example for a design balanced for carryover effects. In this example the subjects are cows and the treatments are the diets provided for the cows. Using the two Latin squares we have three diets A, B, and C that are given to 6 different cows during three different time periods of six weeks each, after which the weight of the milk production was measured. The RCBD utilizes an additive model – one in which there is no interaction between treatments and blocks.

However, in practice only one or two are typically used since more blocking factors requires larger sample sizes to derive significant results. An alternate way of summarizing the design trials would be to use a 4x3 matrix whose 4 rows are the levels of the treatment X1 and whose columns are the 3 levels of the blocking variable X2. The cells in the matrix have indices that match the X1, X2 combinations above. In our previous diet pills example, a blocking factor could be the sex of a patient. And within each of the two blocks, we can randomly assign the patients to either the diet pill (treatment) or placebo pill (control). By blocking on sex, this source of variability is controlled, therefore, leading to greater interpretation of how the diet pills affect weight loss.
Randomized block design still uses ANOVA analysis, called randomized block ANOVA. When participants are placed into a block, we anticipate them to be homogeneous on the control variable, or the blocking variable. In other words, there should be less variability within each block on the control variable, compared to the variability in the entire sample if there were no control variable. Less within-block variability reduces the error term and makes estimate of the treatment effect more robust or efficient, compared to without the blocking variable. Several blocking factors can be combined in a design by nesting—allowing estimation of each blocking factor’s contribution to variance reduction—or crossing—allowing simultaneous removal of several independent sources of variation.
Such interaction is likely caused by other biologically relevant factors that influence the effect of (some) treatments but that have not been accounted for in our experiment and analysis. To do a crossover design, each subject receives each treatment at one time in some order. So, one of its benefits is that you can use each subject as its own control, either as a paired experiment or as a randomized block experiment, the subject serves as a block factor. The smallest crossover design which allows you to have each treatment occurring in each period would be a single Latin square. Often blocking variables are not the variables that we are primarily interested in, but must nevertheless be considered.
For example, consider if the drug was a diet pill and the researchers wanted to test the effect of the diet pills on weight loss. The explanatory variable is the diet pill and the response variable is the amount of weight loss. Although the sex of the patient is not the main focus of the experiment—the effect of the drug is—it is possible that the sex of the individual will affect the amount of weight lost. The Quantitative Reasoning requirement is designed to ensure that students graduate with basic understanding and competency in math, statistics, or computer science. The requirement may be satisfied by exam or by taking an approved course. Learn how to form questions and gather data to explore those questions.
Essentially, this fully crosses the latin square with a new blocking factor and leads to the model specification y ~ drug + Error(rep+device+tech) or y ~ drug + (1|rep) + (1|device) + (1|tech) for Figure 7.15F. Linear mixed models and ‘traditional’ analysis of variance use the same linear model to analyze data from a given design. Their main difference is the way they handle models with multiple variance components. Linear mixed models use different techniques for estimation of the model’s parameters that make use of all available information. Variance estimates are directly available, and linear mixed models do not suffer from problems with unbalanced group sizes. Colloquially, we can say that the analysis of variance approach provides a convenient framework to phrase design questions, while the linear mixed model provides a more general tool for the subsequent analysis.
Other non-statistics UC Berkeley courses, such as IND ENG 172 and EECS 126, cannot be used to fulfill this requirement. Below is a list of sample clusters for students to consider if they would like an idea of courses to combine for their cluster based on a topic of interest. Economics and Business courses are treated as though they are in the same department for purposes of evaluating clusters.
The department has particular strength in Machine Learning, a key ingredient of the emerging field of Data Science. It is also very useful to combine studies of statistics and probability with other subjects. Our department excels at interdisciplinary science, and more than half of the department's undergraduate students are double or triple majors. We note that the sum of squares and the mean square estimates are slightly larger than for the aov() analysis, because the between-block information is taken into account. This provides more power and results in a slightly larger value of the \(F\)-statistic.
The fact that you are missing a point is reflected in the estimate of error. Before high-speed computing, data imputation was often done because the ANOVA computations are more readily done using a balanced design. There are times where imputation is still helpful but in the case of a two-way or multiway ANOVA we generally will use the General Linear Model (GLM) and use the full and reduced model approach to do the appropriate test. Generally the unexplained error in the model will be larger, and therefore the test of the treatment effect less powerful. Another way to think about this is that a complete replicate of the basic experiment is conducted in each block.
Each treatment occurs exactly once per row and once per column and the latin square design imposes two simultaneous constraints on the randomization of drugs on mice. We can think about creating a blocked design by starting from a completely randomized design and ‘splitting’ the experimental unit factor into a blocking and a nested (potentially new) unit factor. Two examples are shown in Figure 7.3, starting from the CRD (Figure 7.3A) randomly allocating drug treatments on mice. In the first RCBD (Figure 7.3B), we create a blocking factor ‘above’ the original experimental unit factor and group mice by their litters. In the second RCBD (Figure 7.3C), we subdivide the experimental unit into smaller units by taking multiple samples per mouse.

No comments:
Post a Comment